2014-11-25

Python format string

Python

Pythonのstringには.format()というフォーマット指定子のメソッドが用意されています．
C言語のsprintfをするときのように，文字列に他の文字を埋め込みたいときに使うやつです．
例えば，次のように使います：

>>> a = 'hoge'
>>> b = 123
>>> c = 3.14
>>> # format指定子
>>> print('a is {0}, b is {1}, and c is {2}.'.format(a,b,c))
>>> # %指定子
>>> print('a is %s, b is %d, and c is %f.' % (a,b,c))

個人的には%指定子のほうをよく使っていたのですが，.formatのほうが柔軟かつ推奨されているということでできるだけ.formatを使うことにしました．
.formatと%の違いで一番大きいことは，.formatでは(おそらく)オブジェクトの__str__メソッドを呼び出して文字列型に変換しているので，ユーザが型を意識せずに単に{0}などと書けば良いのに対し，%では%d,%f,%sなどのようにユーザが型を意識してフォーマットを出力する必要があることだと思います．
.formatのほうがよりダックタイピングらしさがありpythonicで良いっぽい雰囲気です．

.formatで便利そうなTipsをまとめると，

各指定子{0}の数字は省略可能．

>>> print('a is {}, b is {}, and c is {}.'.format('hoge', 123, 3.14))  # この場合，順番が考慮される

各指定子は変数名でアクセス可能(.formatは辞書形式)．

>>> print('a is {a}, b is {b}, and c is {c}.'.format(c=3.14, b=123, a='hoge'))  # この場合，辞書形式なので順番は関係ない

よって，locals()をformatにそのまま投げることで今使っている変数名でそのまま文字列に埋め込み可能．

>>> a = 'hoge'
>>> b = 123
>>> c = 3.14
>>> print('a is {a}, b is {b}, and c is {c}.'.format(**locals()))

便利です*1．

*1:locals()に**している理由：　format()は辞書そのものを引数にはとらない(locals()は辞書を返す)ので，**で辞書を展開する必要があるため．つまり，.format({'a':'hoge', 'b':123})はダメなので，**によって.format(a:'hoge', b:123)へと展開している

2014-11-20

【Google Calendar】Googleカレンダーの背景；日曜日を赤，土曜日を青にする

Firefox

Googleカレンダーの日曜日の行を赤，土曜日の行を青で表示したいときは，
Stylishで次を追加すれば良い：
(If you want to color background of Sundays for red, Saturdays for blue in Google Calendar,
you can add the following code in Stylish:)

@namespace url(http://www.w3.org/1999/xhtml);
@-moz-document url-prefix("http://www.google.com/calendar/"), url-prefix("https://www.google.com/calendar/"){
 
/* background color for day cells; Sundays. */
  div.month-row:nth-child(1) > table:nth-child(1) > tbody:nth-child(1) > tr:nth-child(1) > td:nth-child(1) {
    background: #ffe5e5;
  }
  div.month-row:nth-child(2) > table:nth-child(1) > tbody:nth-child(1) > tr:nth-child(1) > td:nth-child(1) {
    background: #ffe5e5;
  }
  div.month-row:nth-child(3) > table:nth-child(1) > tbody:nth-child(1) > tr:nth-child(1) > td:nth-child(1) {
    background: #ffe5e5;
  }
  div.month-row:nth-child(4) > table:nth-child(1) > tbody:nth-child(1) > tr:nth-child(1) > td:nth-child(1) {
    background: #ffe5e5;
  }
  div.month-row:nth-child(5) > table:nth-child(1) > tbody:nth-child(1) > tr:nth-child(1) > td:nth-child(1) {
    background: #ffe5e5;
  }
  div.month-row:nth-child(6) > table:nth-child(1) > tbody:nth-child(1) > tr:nth-child(1) > td:nth-child(1) {
    background: #ffe5e5;
  }
  
/* background color for day numbers; Sundays.   */
  div.month-row:nth-child(1) > table:nth-child(2) > tbody:nth-child(1) > tr:nth-child(1) > td:nth-child(1){
    background: #ffe5e5;
  }
  div.month-row:nth-child(2) > table:nth-child(2) > tbody:nth-child(1) > tr:nth-child(1) > td:nth-child(1){
    background: #ffe5e5;
  }
  div.month-row:nth-child(3) > table:nth-child(2) > tbody:nth-child(1) > tr:nth-child(1) > td:nth-child(1){
    background: #ffe5e5;
  }
  div.month-row:nth-child(4) > table:nth-child(2) > tbody:nth-child(1) > tr:nth-child(1) > td:nth-child(1){
    background: #ffe5e5;
  }
  div.month-row:nth-child(5) > table:nth-child(2) > tbody:nth-child(1) > tr:nth-child(1) > td:nth-child(1){
    background: #ffe5e5;
  }
  div.month-row:nth-child(6) > table:nth-child(2) > tbody:nth-child(1) > tr:nth-child(1) > td:nth-child(1){
    background: #ffe5e5;
  }
  
/* background color for day cells; Saturdays.  */
  div.month-row:nth-child(1) > table:nth-child(1) > tbody:nth-child(1) > tr:nth-child(1) > td:nth-child(7){
    background: #e5e5ff;
  }
  div.month-row:nth-child(2) > table:nth-child(1) > tbody:nth-child(1) > tr:nth-child(1) > td:nth-child(7){
    background: #e5e5ff;
  }
  div.month-row:nth-child(3) > table:nth-child(1) > tbody:nth-child(1) > tr:nth-child(1) > td:nth-child(7){
    background: #e5e5ff;
  }
  div.month-row:nth-child(4) > table:nth-child(1) > tbody:nth-child(1) > tr:nth-child(1) > td:nth-child(7){
    background: #e5e5ff;
  }
  div.month-row:nth-child(5) > table:nth-child(1) > tbody:nth-child(1) > tr:nth-child(1) > td:nth-child(7){
    background: #e5e5ff;
  }
  div.month-row:nth-child(6) > table:nth-child(1) > tbody:nth-child(1) > tr:nth-child(1) > td:nth-child(7){
    background: #e5e5ff;
  }
  
/* background color for day numbers; Saturdays.  */
  div.month-row:nth-child(1) > table:nth-child(2) > tbody:nth-child(1) > tr:nth-child(1) > td:nth-child(7){
    background: #e5e5ff;
  }
  div.month-row:nth-child(2) > table:nth-child(2) > tbody:nth-child(1) > tr:nth-child(1) > td:nth-child(7){
    background: #e5e5ff;
  }
  div.month-row:nth-child(3) > table:nth-child(2) > tbody:nth-child(1) > tr:nth-child(1) > td:nth-child(7){
    background: #e5e5ff;
  }
  div.month-row:nth-child(4) > table:nth-child(2) > tbody:nth-child(1) > tr:nth-child(1) > td:nth-child(7){
    background: #e5e5ff;
  }
  div.month-row:nth-child(5) > table:nth-child(2) > tbody:nth-child(1) > tr:nth-child(1) > td:nth-child(7){
    background: #e5e5ff;
  }
  div.month-row:nth-child(6) > table:nth-child(2) > tbody:nth-child(1) > tr:nth-child(1) > td:nth-child(7){
    background: #e5e5ff;
  }
}

ちなみに，これは月ビューの一番左の行を赤，右の行を青にしているだけなので，「日曜始まり」かつ「月ごと」の表示にしていないと意味なし．
(Note: because this code simply color the most left to red and most right to blue in monthly-view, please use "monthly-view" and "Sundays most left view".)

2014-11-05

【Python】ふたつの配列からすべての組み合わせを評価

matplotlib numpy Python

引数をふたつとる関数f([x,y])が存在するとします(この場合は引数2つではなく、要素数2の配列をひとつ引数にとるのほうが正しいですが・・・)。
たとえば、f([x,y]) = x+y などです。
このfはうまく実装されているので、f([[1,3], [2,4]])とすると(つまり[1+3, 2+4])、
[f([1,3]), f([2,4])]としたのと同じ効果(つまり[1+3, 2+4])を持ちます(これはnumpyやmatlabならお馴染みの設計だと思います)。

では、この関数fの引数x,yについて、候補が複数あったらどうなるでしょう？
そしてその候補を重複なく選んですべて評価したいときはどうすればよいでしょう？
つまり、x=[1,2,3]、y=[4,5]について、f([1,4]), f([1,5]), f([2,4]), f([2,5]), f([3,4]), f([3,5]) のように評価したいわけです。

ナイーブに考えると、こうなります：

>>> import numpy as np
>>> x = np.array([1,2,3])
>>> y = np.array([4,5])
>>> ret = [f([xi,yi]) for xi in x for yi in y]

しかしこれではせっかくfが引数を行列として処理できるように実装されているのに、それを活かせません。処理速度も遅くなる場合が大半だと思います。
このような場合、numpyのmeshgridが使えます：

>>> xx, yy = np.meshgrid(x, y)
>>> ret = f(np.c_[xx.ravel(), yy.ravel()])

パッと見だと何やってるかよくわかりづらいと思うので解説します。

まず、xx, yy = np.meshgrid(x,y)は、xx = np.tile(x, (len(y),1); yy = np.tile(y, (len(x),1).T; と同じです。サイズがlen(y) X len(x)の行列をふたつ作ります。
先ほどの例で言うと、xx=[[1,2,3],[1,2,3]], yy=[[4,4,4],[5,5,5]]となります。
この時点で、ふたつの行列xx,yyのインデックスi,jを順番に見ていくと、(i,j)=(0,0)のとき[1,4]、(i,j)=(0,1)のとき[2,4]、などとなり、すべての組み合わせを重複なく選べそうになっています。
続いてのxx.ravel(), yy.ravel()ですが、これは単純にxxとyyをバラバラにするだけです。xx.ravelをすると、[1,2,3, 1,2,3], yy.ravel()をすると[4,4,4, 5,5,5]となります。
次にnp.c_[]ですが、これは与えられたオブジェクトの第二軸(second axis)をもとに合体させます。この場合、np.c_[ [1,2,3, 1,2,3], [4,4,4, 5,5,5] ] は、[[1,4],[2,4],[3,4], [1,5],[2,5],[3,5]]となります。
これをfに与えれば、やりたかった重複なくすべての組み合わせの評価ができます。

実際こんなの何に使うのかというと、格子点すべてで関数を評価するときに便利です。
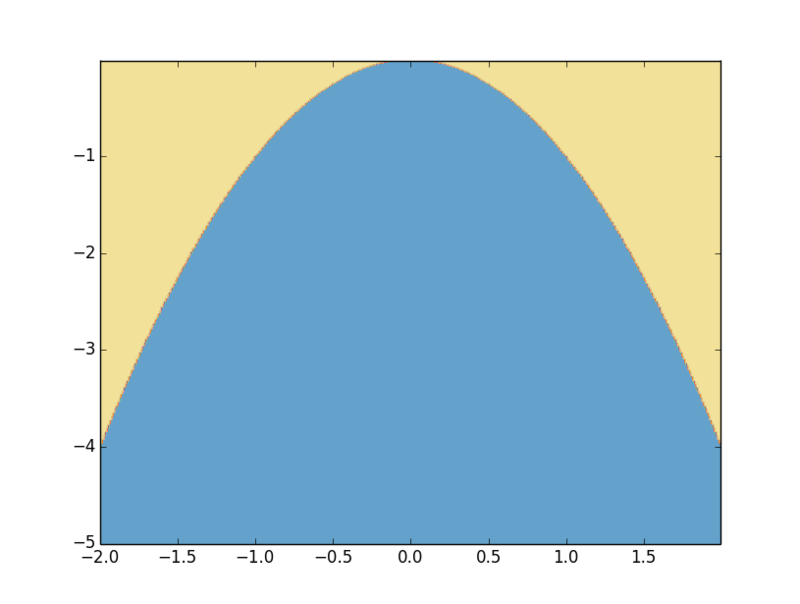
$\begin{align*}y>-x^2\end{align*}$ を視覚化したいとしましょう。これは $\begin{align*}y+x^2>0\end{align*}$ ですから、視覚化するときは、あらゆる(x,y)の組に対して $\begin{align*}y+x^2>0\end{align*}$ が成立すれば黄、しなければ青でグラフを塗りつぶせば良いです。このあらゆる(x,y)の組というのが、np.meshgrid()で作れます。

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> x = np.arange(-2,2, 0.01)
>>> x2 = x**2
>>> y = np.arange(-5,0, 0.01)
>>> xx, yy = np.meshgrid(x2,y)
>>> arg = np.c_[xx.ravel(), yy.ravel()]
>>> ret = np.sum(arg, axis=1)  # calc x^2+y
>>> plt.contourf(x, y, ret.reshape(xx.shape)>0, cmap=plt.cm.Paired, alpha=0.8)
>>> plt.show()

f:id:kaisk:20141105040848p:plain

2014-11-04

【Python】max/minのindex

Python

Pythonでmax/minの値ではなく、そのindexを取るためには、

>>> x = [2, 3, 0, 1]
>>> max_idx = x.index(max(x))
>>> min_idx = x.index(min(x))

みたいな微妙に歯がゆい書き方をしないといけない(しかも、index()とmax()/min()で二回探索しててアホっぽい)のが気になる。
もちろんnumpyにはargmax/argminがあるけど、標準ライブラリレベルで実装してほしい。
matlabみたいに、max()/min()の返り値を最大値／最小値だけじゃなくてそのインデックスとのタプルとかにしちゃえばいいのに・・・(後方互換が完全に消えるからPython3のドサクサにまぎれてやっとけばよかったのに！)

2014-10-30

numpyのshuffleとpermutationの違い

numpy Python

python - shuffle vs permute numpy - Stack Overflow

numpyにはshuffle(x)とpermutation(x)というほぼ同じ機能の関数があります．
どちらも，配列をランダムに並び替えますが，違いが2つあります．

ひとつは，shuffle(x)は配列をin-placeで並び替えるが，permutation(x)は並び替えた配列のコピーを生成するという点です．つまり：

>>> import numpy as np
>>> x = np.array([1,2,3,4,5])
>>> y = np.random.permutation(x)
>>> # y : [3,1,4,2,5]
>>> # x : [1,2,3,4,5]
>>>
>>> x = np.array([1,2,3,4,5])
>>> y = np.random.shuffle(x)
>>> # y : None
>>> # x : [5,2,3,4,1]

もうひとつの違いは，permutation(x)には配列だけでなくint型整数も渡せるという点です．
permutation(5)は，permutation(list(range(5)))と同じ働きをします．(permutation(arange(5))でも同じです．)

2014-10-22

p(x ; y, z)とp(x | y, z)の違い

統計

"The probability of x given y and z"を書くときに， $\begin{align*}p(x;y,z)\end{align*}$ と $\begin{align*}p(x\mid y,z)\end{align*}$ の2種類の表記がある．
上のURLの回答によると，本質的にはどちらも同じ意味らしい．
ただし， $\begin{align*}p(x;y,z)\end{align*}$ は y と z が確率変数でない場合， $\begin{align*}p(x\mid y,z)\end{align*}$ は y と z が確率変数である場合に用いるという使い分けをするのが良い，と主張している人が多くいた．
ただ，どちらにしても，明確な線引きはないようだ．

2014-10-22

マルコフ連鎖モンテカルロ法

統計

マルコフ連鎖モンテカルロ(MCMC)法：
ある時刻 $\begin{align*}i\end{align*}$ の標本 $\begin{align*}\boldsymbol{\theta}_i\end{align*}$ が一つ前の時刻の標本 $\begin{align*}\boldsymbol{\theta}_{i-1}\end{align*}$ に依存して生成されるとき，標本列 $\begin{align*}\boldsymbol{\theta}_{1},\dots,\boldsymbol{\theta}_{n}\end{align*}$ をマルコフ連鎖と呼ぶ．
MCMCでは，まず提案点と呼ばれる標本を生成する．提案点は代理分布 $\begin{align*}p^\prime\end{align*}$ にしたがって発生させる．代理分布は，ガウス分布や一様分布など簡単に生成可能なものが使いやすい．そして標本点を順番に採択・棄却していくことで任意の分布 $\begin{align*}p\end{align*}$ に従う標本を得る．

メトロポリス・ヘイスティングス法という原始的なMCMCでは，次の提案点 $\begin{align*}\boldsymbol{\theta}^\prime\end{align*}$ を生成させる代理分布 $\begin{align*}p^\prime\end{align*}$ のパラメータがひとつ前の標本 $\begin{align*}\boldsymbol{\theta}_{i-1}\end{align*}$ に依存する：
$\begin{align*}\boldsymbol{\theta}^\prime \sim p^\prime(\boldsymbol{\theta} \mid \boldsymbol{\theta}_{i-1})\end{align*}$
この提案点 $\begin{align*}\boldsymbol{\theta}^\prime\end{align*}$ に対して， $\begin{align*}v \sim \text{uniform}[0,1]\end{align*}$ を用いて
$\begin{align*}v \leq \frac{p(\boldsymbol{\theta}^\prime)p^\prime(\boldsymbol{\theta}_{i-1}\mid \boldsymbol{\theta}^\prime)}{p(\boldsymbol{\theta}_{i-1})p^\prime(\boldsymbol{\theta}^\prime\mid \boldsymbol{\theta}_{i-1})}\end{align*}$
が成立するなら提案点 $\begin{align*}\boldsymbol{\theta}^\prime\end{align*}$ を採択し，成立しないなら棄却する．

現在の時刻 $\begin{align*}i\end{align*}$ の標本 $\begin{align*}\boldsymbol{\theta}_i\end{align*}$ は，提案点を採択した時はその提案点となり，棄却したときは前の時刻の標本 $\begin{align*}\boldsymbol{\theta}_{i-1}\end{align*}$ となる．

初期値 $\begin{align*}\boldsymbol{\theta}_0\end{align*}$ は適当に決定する必要がある．
収集した標本列 $\begin{align*}\{\boldsymbol{\theta}_i\}_{i=1}^n\end{align*}$ の最初の方は初期値に依存してしまうため，最初のほうを捨てることがある．これを焼き入れと呼ぶ．

代理分布 $\begin{align*}p^\prime(\boldsymbol{\theta}\mid\boldsymbol{\theta}_{i-1})\end{align*}$ には，例えば期待値が $\begin{align*}\boldsymbol{\theta}_{i-1}\end{align*}$ のガウス分布を用いる．このガウス分布は，最も最近採択された標本の近くから提案点を生成することになる．

keisukeのブログ

乱雑です！自分用のメモです！統計や機械学習の勉強と、読み物を書く練習と、備忘録用のブログ