scipy.stats - scipyの統計関数群のAPI
scipyにはstatsという統計関数をまとめたモジュールがあります. statsにはいろいろな統計関数が用意されていますが,APIは統一されていますので,それについてちょっとまとめてみます.
どんな統計関数があるの?
かなりの種類があり,すべてを書くわけにはいかないので, 公式のリファレンスへのリンクを置いておきます.
API
各統計関数は,scipy.stats.hogeとしてアクセスできます.
例えば,正規分布なら,scipy.stats.normです.
APIはすべての統計関数で共通なので,以下では正規分布の例を使います.
from scipy.stats import norm # 正規分布
rvs (Random variates) 確率変数
x = norm.rvs(loc=0, scale=1, size=1)
期待値loc,標準偏差scaleの正規分布に従う確率変数をsize個ランダムに取得します.
pdf (Probability density function) 確率密度関数

norm.pdf(x=1.0, loc=0, scale=1)
期待値loc,標準偏差scaleの正規分布の確率密度関数のx=1.0での値を取得します.
ただし,離散確率分布(binom等)の場合,pdfではなくpmf (Probability mass function) となります.
cdf (Cumulative density function) 累積分布関数
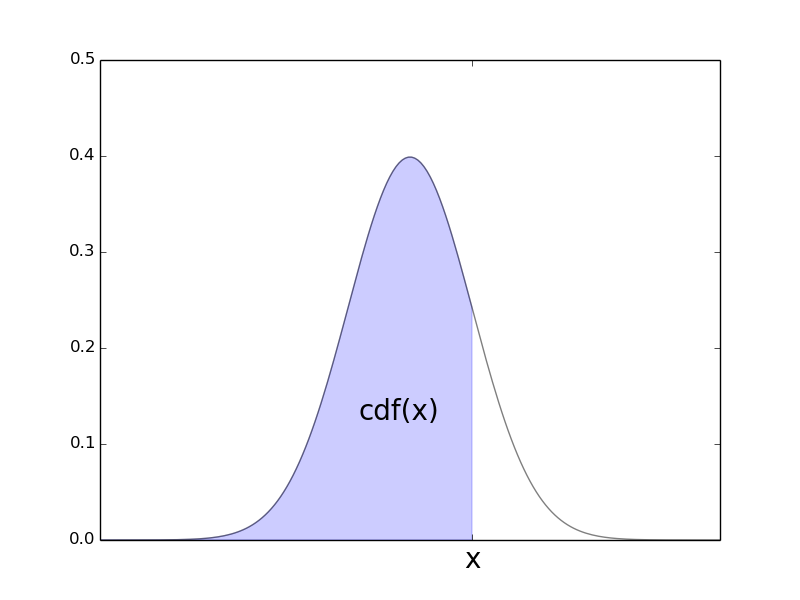
norm.cdf(x=1.0, loc=0, scale=1)
期待値loc,標準偏差scaleの正規分布の累積分布関数のx=1.0での値を取得します.
sf (Survival function) 生存関数

norm.sf(x=1.0, loc=0, scale=1)
期待値loc,標準偏差scaleの正規分布の生存関数のx=1.0での値を取得します.
生存関数sfは,1-cdf と同じです.
ppf (Percent point function) パーセント点関数

norm.ppf(q=0.84, loc=0, scale=1)
期待値loc,標準偏差scaleの正規分布のパーセント点関数のq=0.84での値を取得します.
パーセント点関数ppfは,cdfの逆関数です.
よって,ppf(0.25)は第1四分位点,ppf(0.75)は第3四分位点,ppf(0.5)は第2四分位点(すなわちメディアン)です.
isf (Inverse survival function) 生存関数の逆関数

norm.isf(q=0.16, loc=0, scale=1)
期待値loc,標準偏差scaleの正規分布の生存関数の逆関数のq=0.16での値を取得します.
よって,isf(0.25)は第3四分位点,isf(0.75)は第1四分位点,isf(0.5)は第2四分位点(すなわちメディアン)です.
interval

a,b = norm.interval(alpha=0.95, loc=0, scale=1)
期待値loc,標準偏差scaleの正規分布のalpha=0.95ぶんだけの分布が含まれる範囲を,メディアンを中心にとって取得します.
frozen RV object
各APIは,scipy.stats.norm.xxx(x, loc, scale)のような形をしていますが,パラメータlocとscaleを固定したオブジェクトを作ることができます:
import scipy.stats # direct call print(scipy.stats.norm.pdf(0, loc=0, scale=1)) # 0.3989 # frozen RV object rv = scipy.stats.norm(loc=0, scale=1) print(rv.pdf(0)) # 0.3989
このふたつの例はどちらも「期待値0・分散1の正規分布の確率密度関数のx=0における値」を計算しています.
後者の例では,一旦rvというオブジェクトを生成しています:
これはloc=0, scale=1という値が与えられた正規分布のオブジェクトになっています.
このように,分布に対するパラメータ(ハイパーパラメータ,正規分布ならば期待値locと標準偏差scale)をあらかじめ与えたfrozen RV objectを用いることで,同じパラメータの分布を何度も使いまわすことが簡単になります.